Q Learning

Training Loop

1. Compute Action and use epsilon greedy

• If np.random.random()<epsilon, Choose a random action
  action = torch.tensor(random.randint(0, self.num_actions - 1))
• Else choose from critic network
  action = self.critic(observation).argmax(dim=1)

2. Step environment

3. Add data to replay buffer
   replay_buffer.insert(...)

4. Sample from replay buffer
   batch = replay_buffer.sample(config["batch_size"])

5. Train agent, we update the target critic network only every fixed timestep and the critic network every timestep

• If step % self.target_update_period == 0:
  Update target critic network
  self.target_critic.load_state_dict(self.critic.state_dict())
• Update critic network
  self.update_critic(obs, action, reward, next_obs, done)

Update Critic

1. Compute all options of q_values
   next_qa_values = self.target_critic(next_obs)
2. Choose q_values: If using Double Q,

# Use critic network to update actions
next_actions = self.critic(next_obs).argmax(dim=1)
# Choose the Q values based on actions
next_q_values = next_qa_values.gather(1, next_actions.unsqueeze(-1)).squeeze(-1)

• Else just use the max Q values
  next_q_values = next_qa_values.max(dim=1).values

3. Compute target_values
   target_values = reward+self.discount*next_q_values*(~done)

4. Get q_values from critic network
   q_values = self.critic(obs).gather(1, action.unsqueeze(-1)).squeeze(-1)

5. Compute loss function
   loss = self.critic_loss(q_values, target_values)

6. Update critic network

self.critic_optimizer.zero_grad()
# Gradient clipping
loss.backward()
self.critic_optimizer.step()

Experiments to Run

# Cartpole
python cs285/scripts/run_hw3_dqn.py -cfg experiments/dqn/cartpole.yaml

# Lunar_Lander
python cs285/scripts/run_hw3_dqn.py -cfg experiments/dqn/lunarlander.yaml --seed 1
python cs285/scripts/run_hw3_dqn.py -cfg experiments/dqn/lunarlander.yaml --seed 2
python cs285/scripts/run_hw3_dqn.py -cfg experiments/dqn/lunarlander.yaml --seed 3


# double q
python cs285/scripts/run_hw3_dqn.py -cfg experiments/dqn/lunarlander_doubleq.yaml --seed 1
python cs285/scripts/run_hw3_dqn.py -cfg experiments/dqn/lunarlander_doubleq.yaml --seed 2
python cs285/scripts/run_hw3_dqn.py -cfg experiments/dqn/lunarlander_doubleq.yaml --seed 3




# Pacman
python cs285/scripts/run_hw3_dqn.py -cfg experiments/dqn/mspacman.yaml
python cs285/scripts/run_hw3_dqn.py -cfg experiments/dqn/mspacman_lr_3e-4.yaml
python cs285/scripts/run_hw3_dqn.py -cfg experiments/dqn/mspacman_lr_5e-4.yaml
python cs285/scripts/run_hw3_dqn.py -cfg experiments/dqn/mspacman_lr_5e-5.yaml

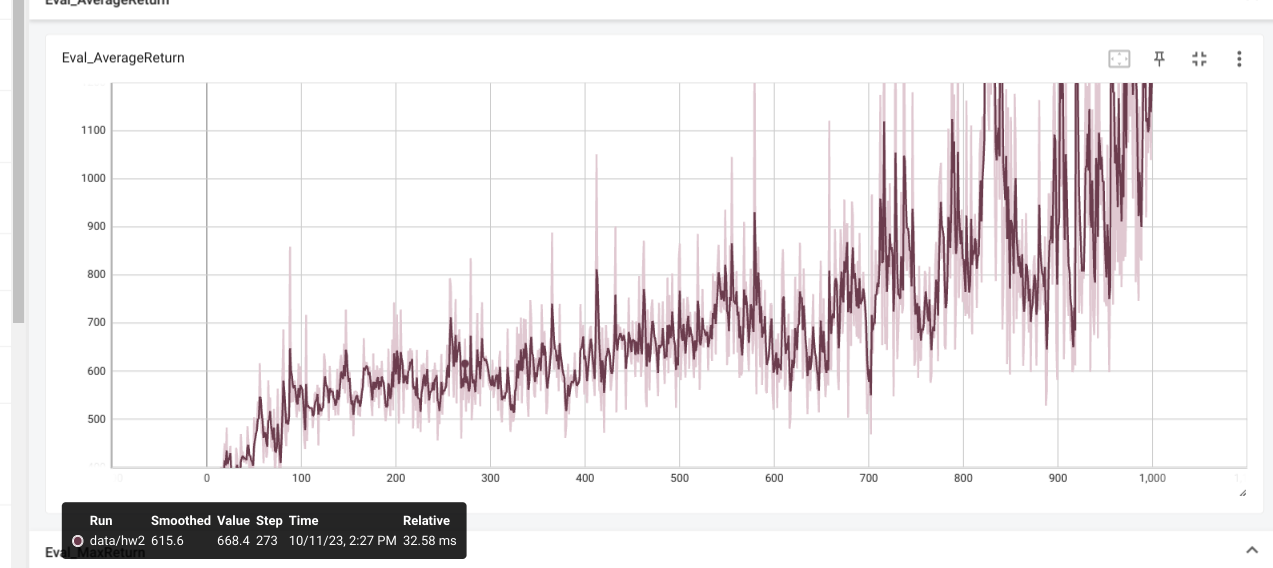
Results

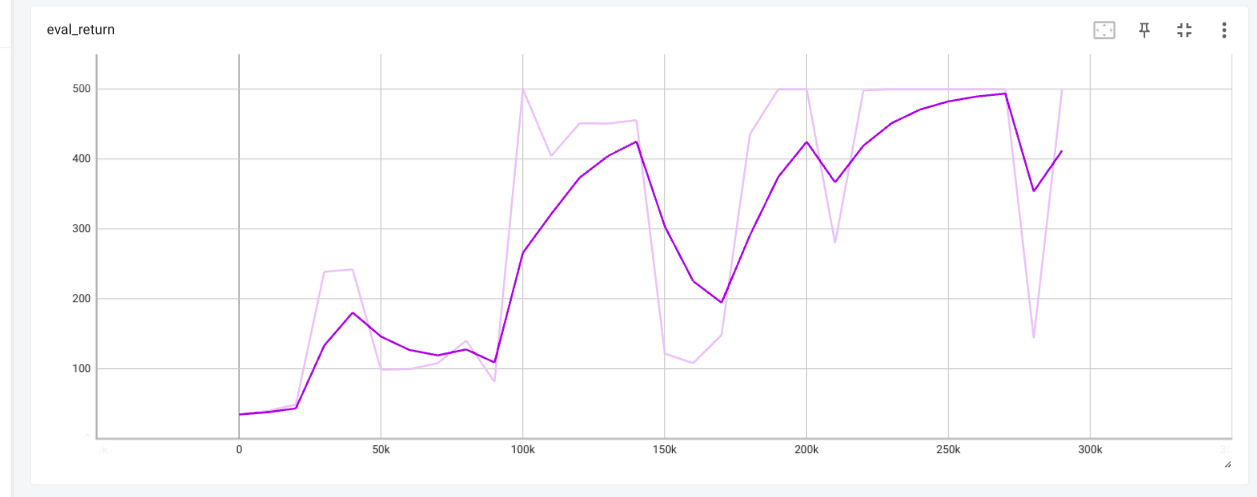
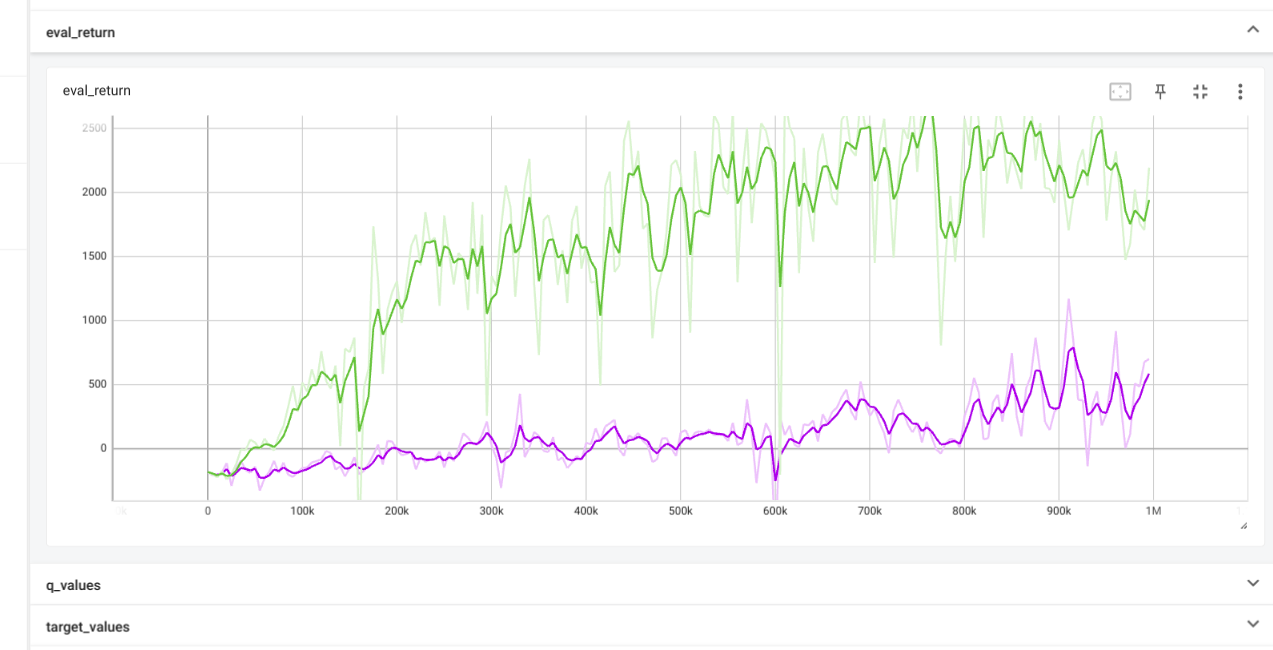
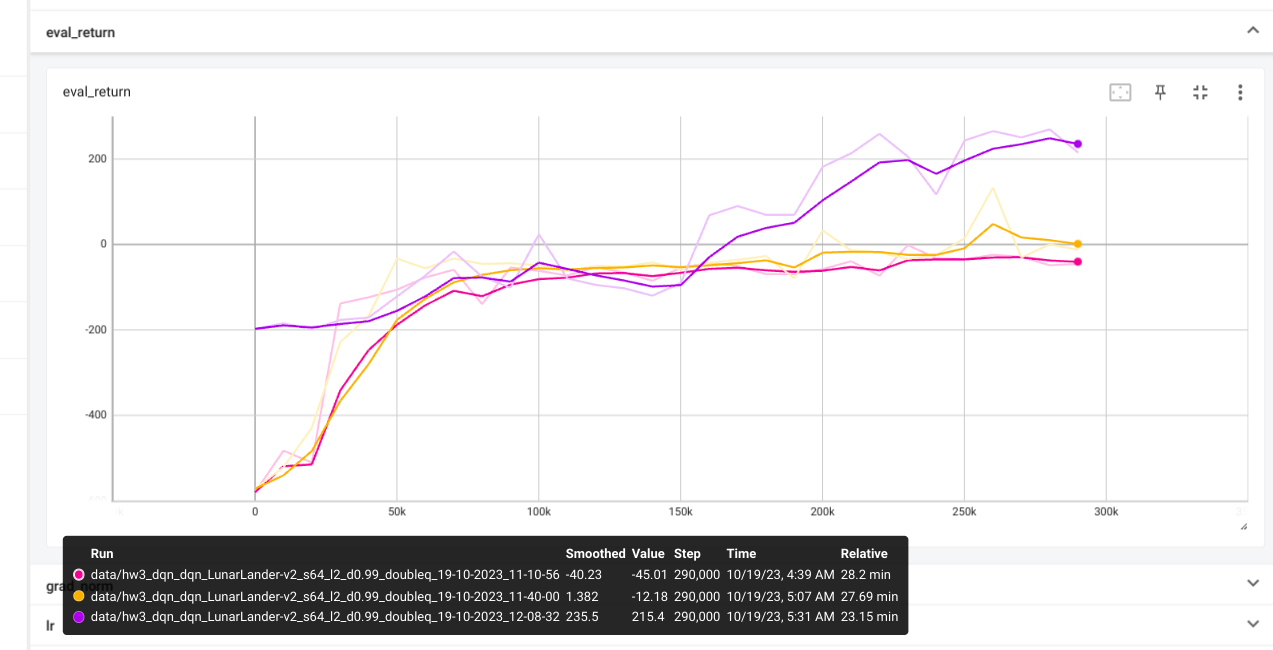
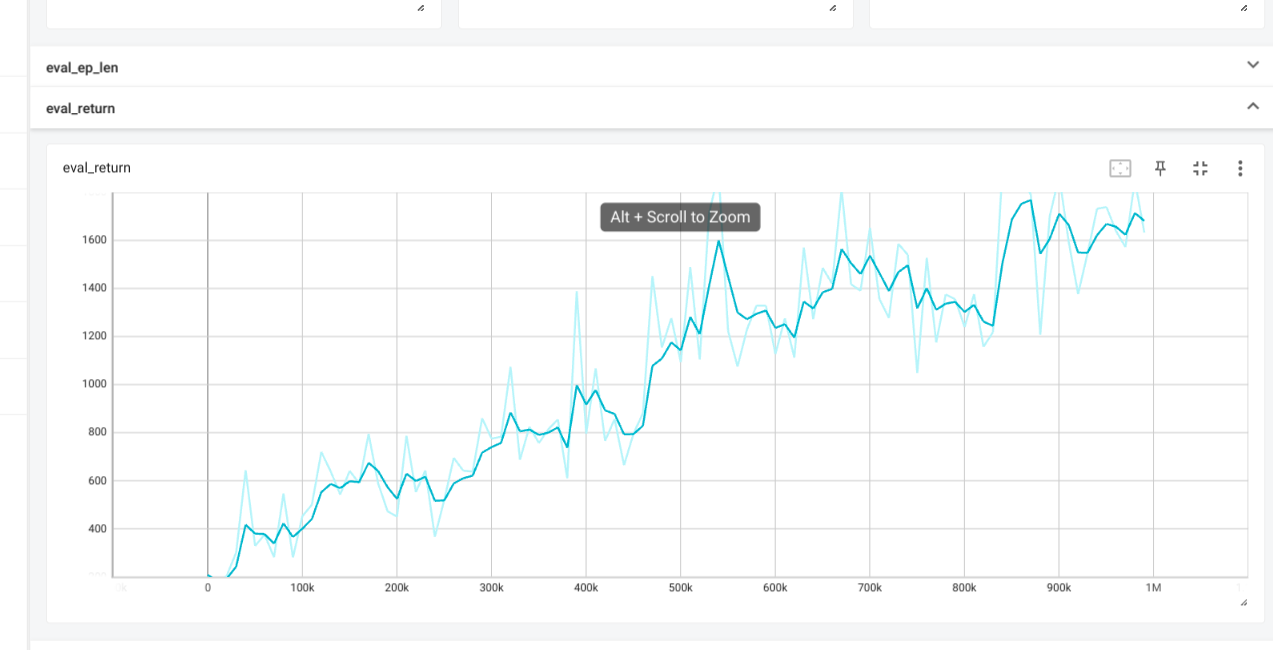
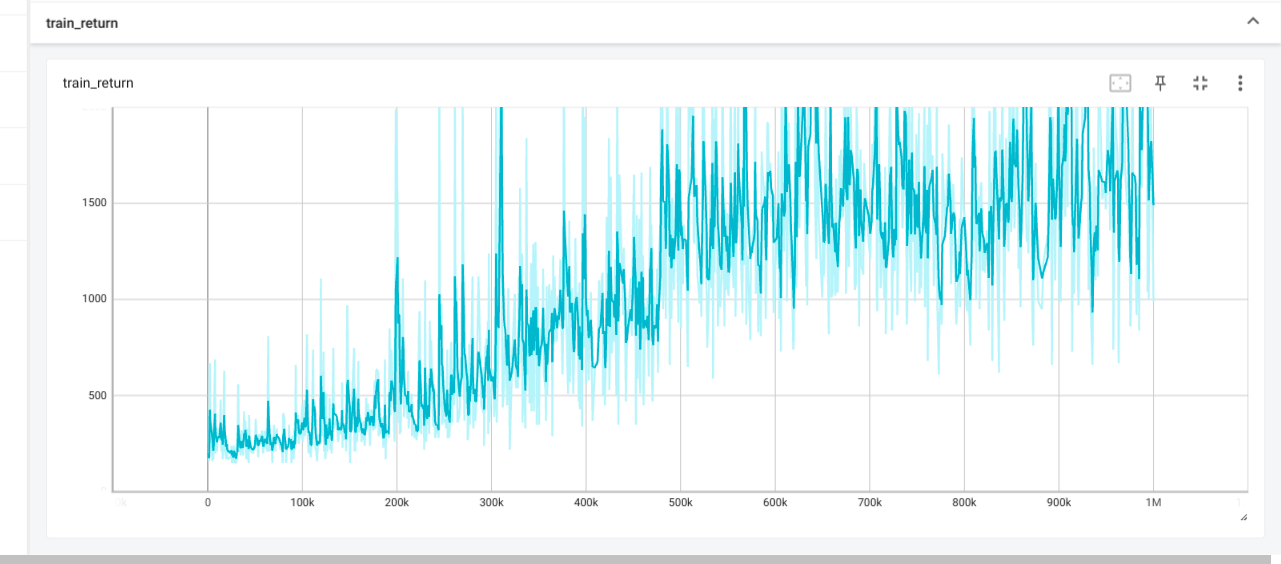
If learning rate of CartPole is too high then the predicted q values and
critic error are both very high, leaing to overestimation.

SAC

Training Loop

1. Compute Action

• Random sampling(at first)
  action = env.action_space.sample()

2. Step environment
3. Add data to replay buffer
4. Sample a batch from replay buffer
5. Train agent by updating actor and critic

Normally we use 1 critic.In SAC we use 2 critics and on every fixed timestep we soft update the target critic target_param.data.copy_(target_param.data * (1.0 - tau) + param.data * tau) , in math soft updates $φ′ ← φ′ + τ (φ − φ′)$

Entropy

Objective function for policy with entropy bonus.

$$H(\pi(a|s)) = \mathbb{E}\_{a\sim\pi} [-\log \pi(a|s)]$$

In code
-action_distribution.log_prob(action_distribution.rsample()).mean()

Update Critic

1. Get Actor Distribution
2. Sample from actor
3. Get q_values

• Double-Q(switch to reduce variance)

$$y*A = r + \gamma Q*{\phi'_B} (s', a')$$

$$y_B = r + \gamma Q_{\phi'\_A} (s', a')$$

• Clipped double-Q:

$$y*A = y_B = r + \gamma \min(Q*{\phi'_A} (s', a'), Q_{\phi'\_B} (s', a'))$$

4. Compute Entropy(if used)

$$y \leftarrow r*t + \gamma(1 - d_t) [Q*\phi(s*{t+1}, a*{t+1}) + \beta H(\pi(a*{t+1}|s*{t+1}))]$$

$d_t$ is a binary value (0 or 1)

5. Compute the target Q-value

REINFORCE

Actor with REINFORCE

$$\mathbb{E}_{s\sim D,a\sim \pi(a|s)} [\nabla_\theta \log(\pi*\theta (a|s))Q*\phi(s, a)]$$

REPARAMETRIZE

Actor with REPARAMETRIZE

Objective function for policy with entropy bonus.

$$L*\pi = Q(s, \mu*\theta (s) + \sigma\_\theta (s)\varepsilon) + \beta H(\pi(a|s))$$

In code: loss -= self.temperature * entropy

Experiments to Run

# SAC
# HalfCheetah
python cs285/scripts/run_hw3_sac.py -cfg experiments/sac/halfcheetah_reinforce1.yaml
python cs285/scripts/run_hw3_sac.py -cfg experiments/sac/halfcheetah_reinforce10.yaml
python cs285/scripts/run_hw3_sac.py -cfg experiments/sac/halfcheetah_reparametrize.yaml


# Hopper
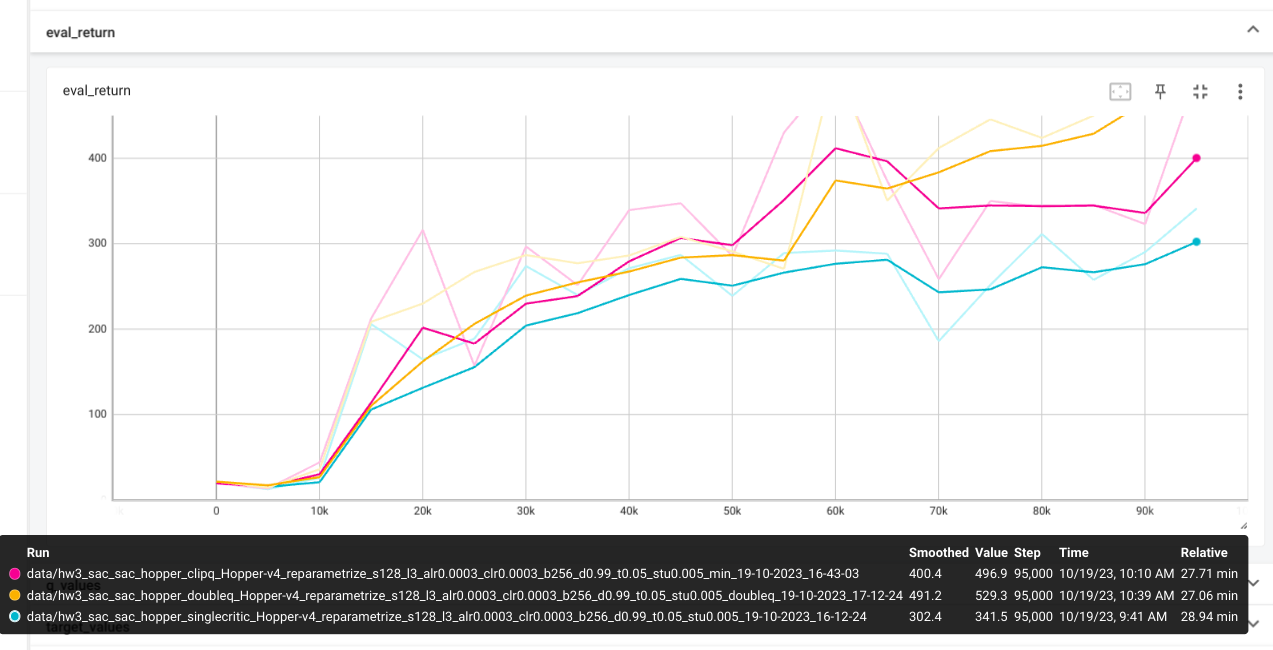
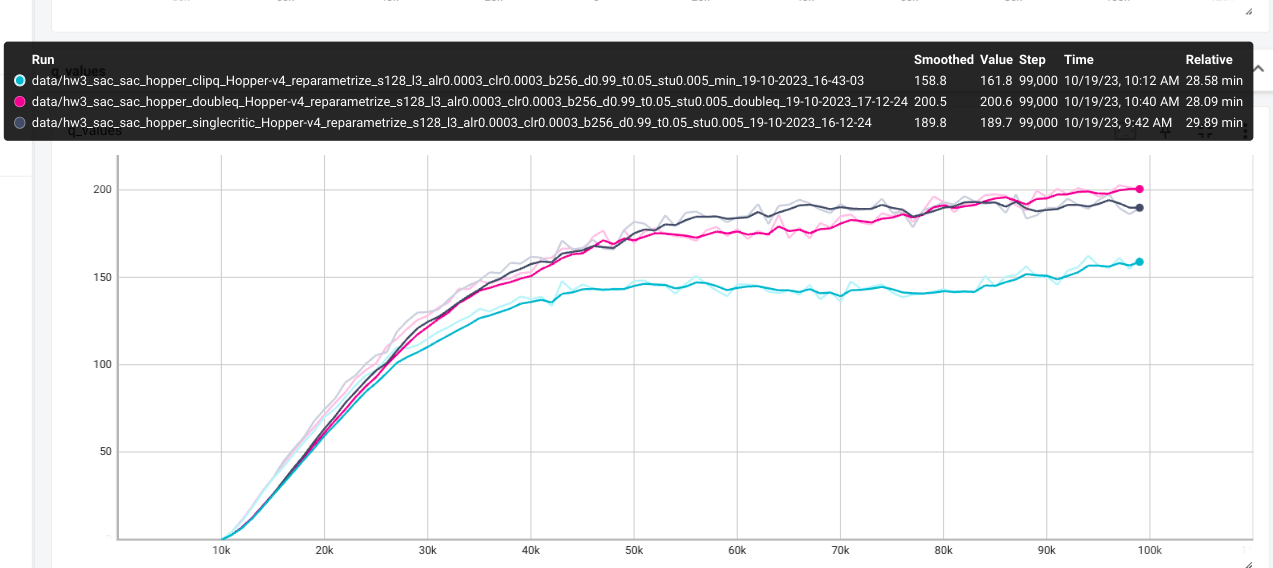
python cs285/scripts/run_hw3_sac.py -cfg experiments/sac/hopper.yaml
python cs285/scripts/run_hw3_sac.py -cfg experiments/sac/hopper_clipq.yaml
python cs285/scripts/run_hw3_sac.py -cfg experiments/sac/hopper_doubleq.yaml


# Humanoid
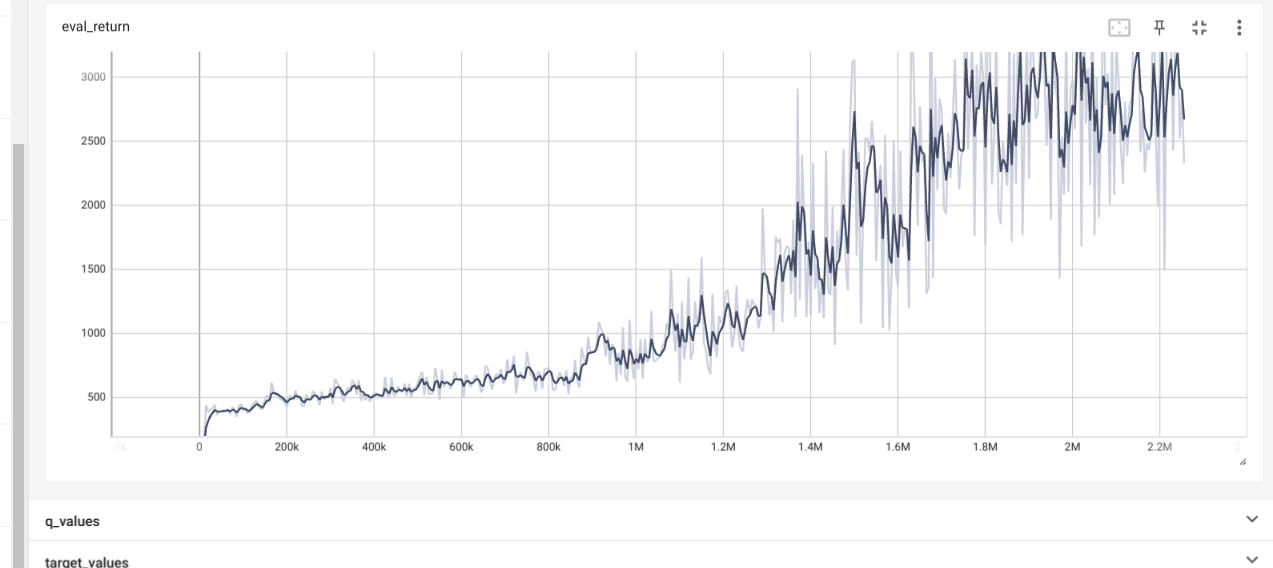
python cs285/scripts/run_hw3_sac.py -cfg experiments/sac/humanoid.yaml

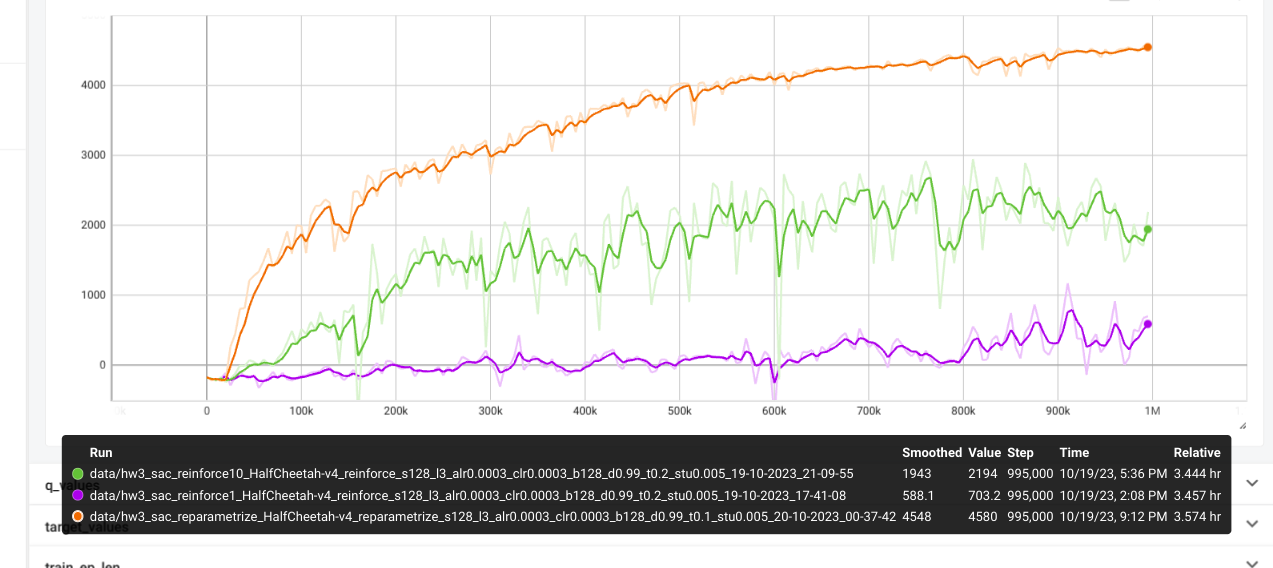
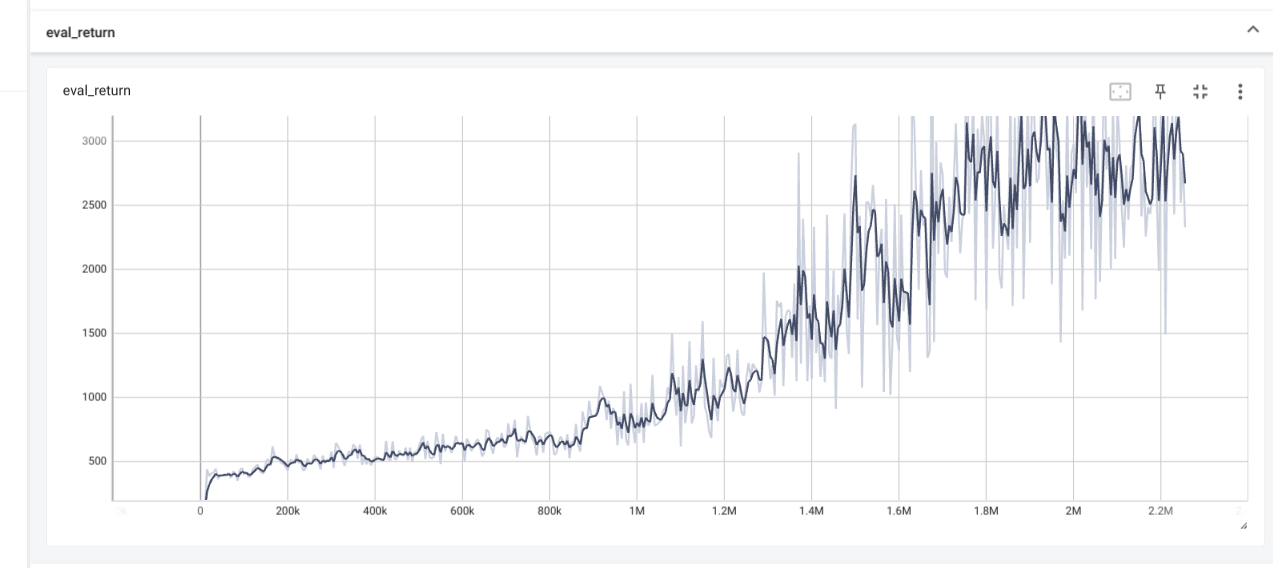
Results

The Q_values tend to be more stable with clipq. Singleq overestimates
Q_values. Thus singleq tend todrop in performances.