November 20, 2023 • 872 words

Policy Gradients

Full Trajectory vs Reward to Go

There are 2 kinds of estimator for Policy Gradients, full trajectory and and "reward-to-go"

We run the two configs on Cartpole with different parameters, specifically, rtg means reward to go, na means normalizing the advantages.

Normalizing:

if self.normalize_advantages:
    advantages = (advantages - np.mean(advantages)) / (np.std(advantages) + 1e-8)

Discounted Return

ParseError: KaTeX parse error: Undefined control sequence: \* at position 167: …ma^{t'} r(s*{it\̲*̲}, a*{it'}) 

total_discounted_return = sum(self.gamma ** i * rewards[i] for i in range(len(rewards)))
discounted_rewards= [total_discounted_return] * n

Discounted Reward-to-go

ParseError: KaTeX parse error: Undefined control sequence: \* at position 169: …^{t*-t} r(s*{it\̲*̲}, a*{it\*}) 

running_add = 0
for t in reversed(range(len(rewards))):
    running_add = running_add * self.gamma + rewards[t]
    discounted_rewards[t] = running_add

CartPole

# small batch
python cs285/scripts/run_hw2.py --env_name CartPole-v0 -n 100 -b 1000 --exp_name cartpole
python cs285/scripts/run_hw2.py --env_name CartPole-v0 -n 100 -b 1000 -rtg --exp_name cartpole_rtg
python cs285/scripts/run_hw2.py --env_name CartPole-v0 -n 100 -b 1000 -na --exp_name cartpole_na
python cs285/scripts/run_hw2.py --env_name CartPole-v0 -n 100 -b 1000 -rtg -na --exp_name cartpole_rtg_na

#large batch
python cs285/scripts/run_hw2.py --env_name CartPole-v0 -n 100 -b 4000 --exp_name cartpole_lb
python cs285/scripts/run_hw2.py --env_name CartPole-v0 -n 100 -b 4000 -rtg --exp_name cartpole_lb_rtg
python cs285/scripts/run_hw2.py --env_name CartPole-v0 -n 100 -b 4000 -na --exp_name cartpole_lb_na
python cs285/scripts/run_hw2.py --env_name CartPole-v0 -n 100 -b 4000 -rtg -na --exp_name cartpole_lb_rtg_na

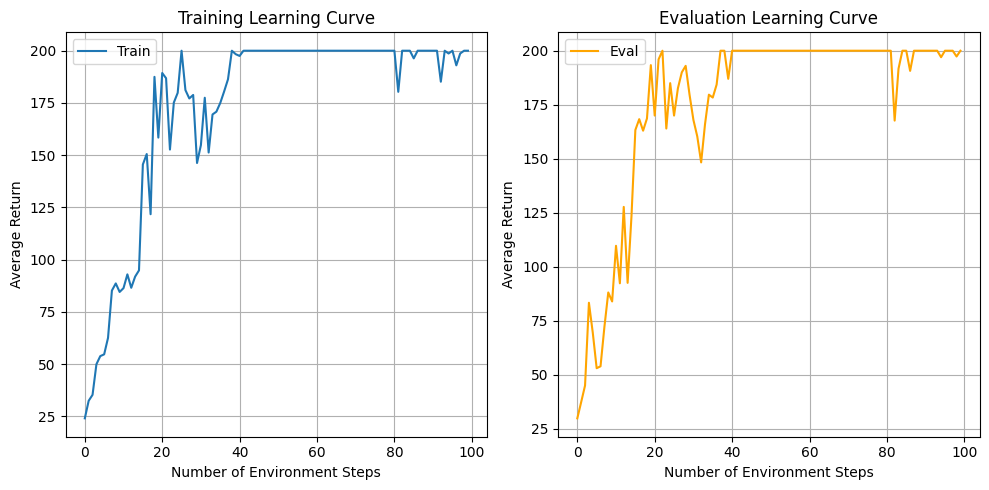
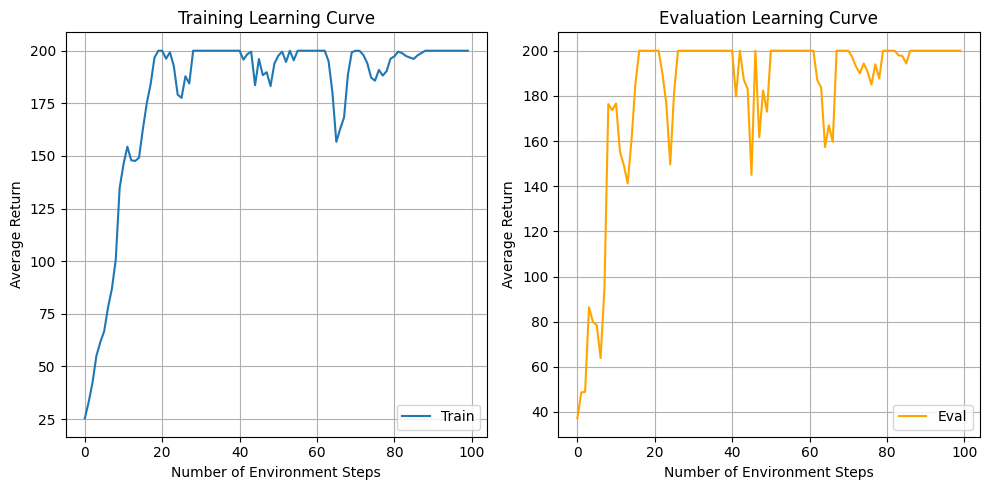
alt text

alt text

  • Q: Which value estimator has better performance without advantage
    normalization?
  • A: Without advantage normalization, rtg performs much better than
    default.
  • Q: Did advantage normalization help?
  • A: Yes, advantage normalization helps reduce variance, leading to
    average returns being more stable
  • Q: Did the batch size make an impact?
  • A: While small batch lead to fewer environment steps to converge, large
    batch has less variance after initially reaching 200.

State Dependent Baseline

We now implement value functions to approximate the sum of future rewards with a particular state

No baseline: advantages = q_values

With baseline:

Vϕπ(st)≈∑t′=tT−1Eπθ[r(st′,at′)∣st]V^{\pi}_{\phi}(s_t) \approx \sum_{t'=t}^{T-1} \mathbb{E}_{\pi_\theta} [r(s_{t'},a_{t'})|s_t]

We run the value network self.critic(obs), so that advantages = q_values - values

HalfCheetah

# No baseline
python cs285/scripts/run_hw2.py --env_name HalfCheetah-v4 -n 100 -b 5000 -rtg --discount 0.95 -lr 0.01 --exp_name cheetah
#add -na
python cs285/scripts/run_hw2.py --env_name HalfCheetah-v4 -n 100 -b 5000 -rtg --discount 0.95 -lr 0.01 --exp_name cheetah_na -na
# Baseline
python cs285/scripts/run_hw2.py --env_name HalfCheetah-v4 -n 100 -b 5000 -rtg --discount 0.95 -lr 0.01 --use_baseline -blr 0.01 -bgs 5 --exp_name cheetah_baseline
# Baseline na
python cs285/scripts/run_hw2.py --env_name HalfCheetah-v4 -n 100 -b 5000 -rtg --discount 0.95 -lr 0.01 --use_baseline -blr 0.01 -bgs 5 --exp_name cheetah_baseline -na
# Customized
python cs285/scripts/run_hw2.py --env_name HalfCheetah-v4 -n 100 -b 5000 -rtg --discount 0.95 -lr 0.01 --use_baseline -blr 0.01 -bgs 3 --exp_name cheetah_baseline_low_bgs
python cs285/scripts/run_hw2.py --env_name HalfCheetah-v4 -n 100 -b 5000 -rtg --discount 0.95 -lr 0.01 --use_baseline -blr 0.005 -bgs 5 --exp_name cheetah_baseline_low_blr

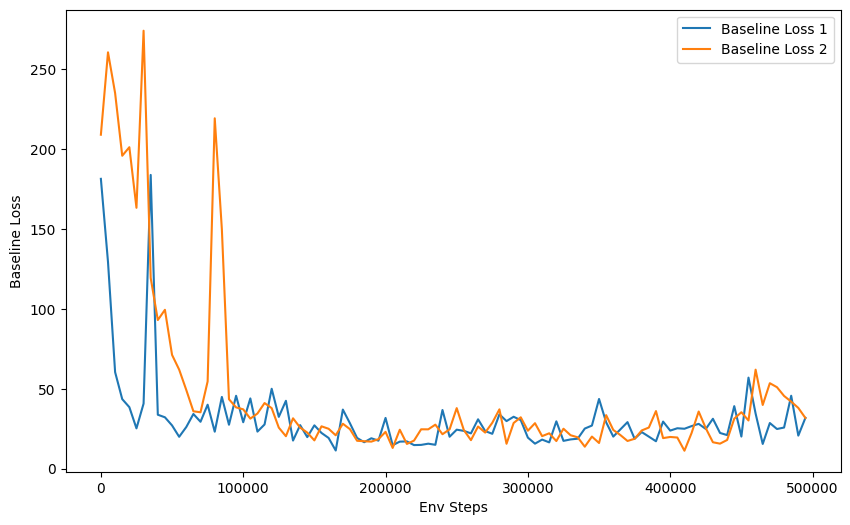
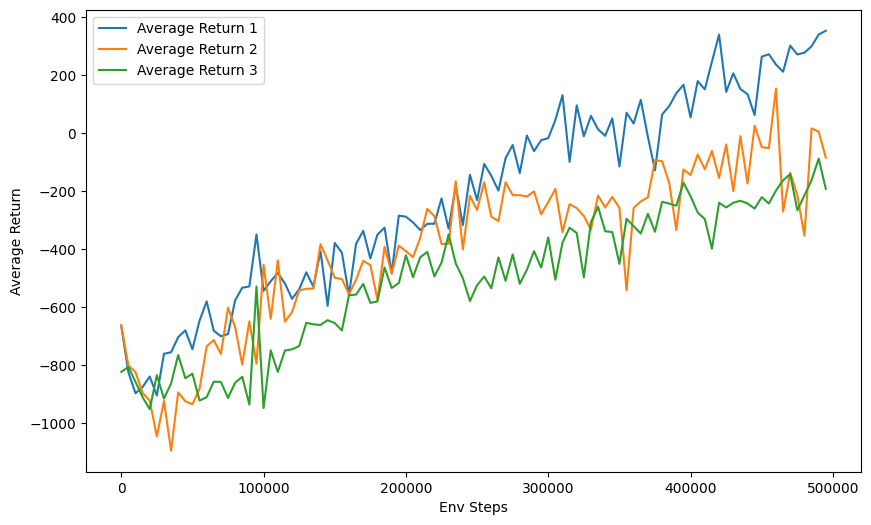
alt text

alt text

  • Normalizing advantages makes learning faster.
  • With a decreased number of bgs or blr, the half cheetah tends to be
    similar in performance.
  • The default(without normalizing advantages or baseline) performs
    poor

Baseline with GAE

We can further reduce variance by using GAE after baseline

use a combination of n-step returns and VϕπV_{\phi}^{\pi}

Aπ(s∗t,at)≈δt=r(st,at)+γVπ∗ϕ(s∗t+1)−Vπ∗ϕ(s∗t)=∑∗t′=tt+nγt′−tr(s∗t′,a∗t′)+γnVϕπ(st+n+1)−Vπ_ϕ(st)A^{\pi}(s*t, a_t) \approx \delta_t = r(s_t, a_t) + \gamma V^{\pi}*{\phi}(s*{t+1}) - V^{\pi}*{\phi}(s*t) = \sum*{t'=t}^{t+n} \gamma^{t'-t}r(s*{t'},a*{t'}) + \gamma^n V^{\pi}_{\phi}(s_{t+n+1}) - V^{\pi}\_{\phi}(s_t)

Generalized Advantage Estimation (GAE):

We can combine multiple n-step advantage estimates as an exponentially weighted sum

As tt goes to infinity, a Recursive derivation of GAE:

AGAEπ(st,at)=δt+γλAGAEπ(s∗t+1,a∗t+1)A^{\pi}_{\text{GAE}}(s_t,a_t) = \delta_t + \gamma\lambda A^{\pi}_{\text{GAE}}(s*{t+1},a*{t+1}) 

for i in reversed(range(obs.shape[0])):
    delta = rewards[i] + self.gamma * values[i + 1] * (1 - terminals[i]) - values[i]
    advantages[i]=delta + self.gamma * self.gae_lambda * (1 - terminals[i])* advantages[i + 1]

LunarLander-v2

python cs285/scripts/run_hw2.py --env_name LunarLander-v2 --ep_len 1000 --discount 0.99 -n 300 -l 3 -s 128 -b 2000 -lr 0.001 --use_reward_to_go --use_baseline --gae_lambda 0    --exp_name lunar_lander_lambda0
python cs285/scripts/run_hw2.py --env_name LunarLander-v2 --ep_len 1000 --discount 0.99 -n 300 -l 3 -s 128 -b 2000 -lr 0.001 --use_reward_to_go --use_baseline --gae_lambda 0.95 --exp_name lunar_lander_lambda0.95
python cs285/scripts/run_hw2.py --env_name LunarLander-v2 --ep_len 1000 --discount 0.99 -n 300 -l 3 -s 128 -b 2000 -lr 0.001 --use_reward_to_go --use_baseline --gae_lambda 0.98 --exp_name lunar_lander_lambda0.98
python cs285/scripts/run_hw2.py --env_name LunarLander-v2 --ep_len 1000 --discount 0.99 -n 300 -l 3 -s 128 -b 2000 -lr 0.001 --use_reward_to_go --use_baseline --gae_lambda 0.99 --exp_name lunar_lander_lambda0.99
python cs285/scripts/run_hw2.py --env_name LunarLander-v2 --ep_len 1000 --discount 0.99 -n 300 -l 3 -s 128 -b 2000 -lr 0.001 --use_reward_to_go --use_baseline --gae_lambda 1.00 --exp_name lunar_lander_lambda1
  • λ = 0.95 (blue line) performs poorly, with low returns and high
    variance compared to other values.
  • λ = 0.98 (orange line) and λ = 0.99 (green line) perform well, but λ
    = 0.99 experiences a significant drop towards the end.
  • λ = 0 (red line) shows high variance and lower overall returns,
    suggesting that not accounting for future rewards is less effective.
    The advantage estimate becomes the same as the TD (Temporal
    Difference) error.
  • λ = 1 (purple line) has an early rise in returns and exhibits high
    variance, indicating that overemphasizing long-term rewards can lead
    to unstable learning.

Inverted Pendulum

# finetuning
for seed in $(seq 1 5); do python cs285/scripts/run_hw2.py --env_name InvertedPendulum-v4 -n 200 --exp_name pendulum_default_s$seed --use_baseline -na -rtg --discount 0.95 --n_layers 2 --layer_size 16 --gae_lambda 0.98 --batch_size 1000 -lr 0.02 --seed $seed; done

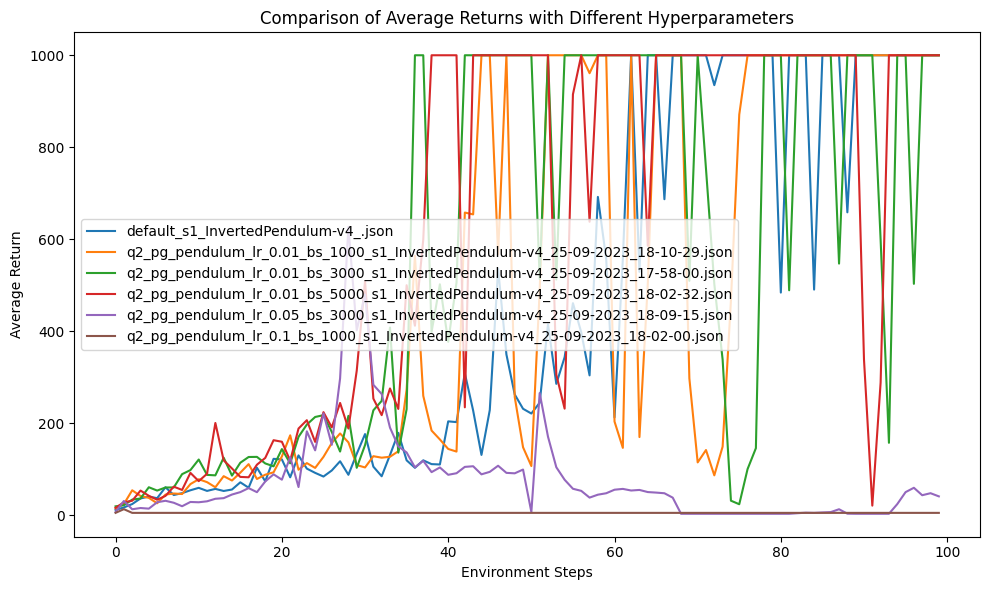
alt text

Humanoid

python cs285/scripts/run_hw2.py --env_name Humanoid-v4 --ep_len 1000 --discount 0.99 -n 1000 -l 3 -s 256 -b 50000 -lr 0.001 --baseline_gradient_steps 50 -na --use_reward_to_go --use_baseline --gae_lambda 0.97 --exp_name humanoid --video_log_freq 5

Loading...




Loading...